九个问题
01背包- 完全背包
- 多重背包
- 混合背包
- 二维混合背包
- 分组背包
- 背包问题求方案熟
- 求背包问题的方案
- 有依赖的背包
感谢: https://www.youtube.com/watch?v=nleY0-eexps
01背包
问题描述
问题描述
有N件物品和一个容量V的背包,第i件物品体积vi,价值是wi.
求解将那些物品装入背包,可是这些物品总体积不超过背包容量,且总价值最大
输入格式
第一行两个整数, N和V, 用空格隔开, 分别表示物品数量和背包容积
接下来有N行, 每行有两个整数vi, wi, 分别表示第i件物品的体积和价值
输出格式
一个整数, 表示最大价值
数据范围
0 < N, V <1000
0 < vi, wi < 1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
算法分析
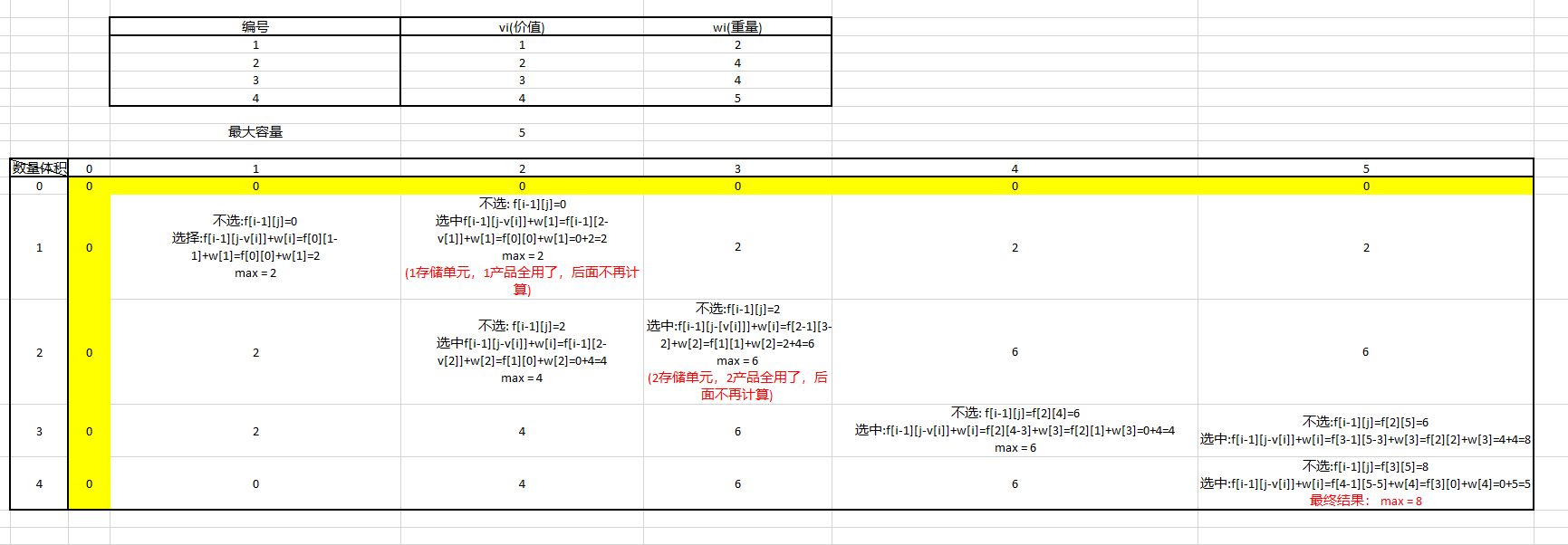
我们用一个二维数组f[n][m]存储所有状态,n表示商品总数,m表示背包容量。m,n > 0
f[i][j]表示只考虑前i个物品,总体积是j的情况下,总价值最大是多少i,j取值范围0<i<=n, 至少一个商品,之多n个商品; 0<=j<=m,重量最小可以是0(刚好用完),最大可以是m
如何求解f[i][j]? 对于每一个f[i][j], 我们哟两种选择, 不选择它或者选泽它。
-
不选第i个商品。那么当前总价值和上一行当前重量下结果是一样的。
f[i][j] = f[i-1][j] -
选择第i个商品。如果要选择当前商品,那么首先获得w[i]价值; 同时,我们要知道剩余空间可承载的最大价值
f[i-1][j-v[i]]表示i-1商品情况下,当前剩余空间j-v[i]中最大能装多少价值的物品
所以,结果就是
f[i][j] = f[i-1][j-v[i]] + w[i] -
最终结果
result = max(f[N][0~V]) 在所有N个商品最多占用V体积的情况下,最大总价值
后面我们会发现,其实f[n][m]就是最大价值
初始化
f[0][0] = 0 考察0个物品,总体积是0的时候,总价值是0
算法复杂度: O(n^2) NV = 10001000 = 1,000,000
演算
算法实现
#include <iostream>
#include <cstring>
#include <algorithm>
#include <fstream>
#include <sstream>
using namespace std;
#define MAX_LINE_LENGTH 256
const int N = 1000;
int n, m;
int f[N][N];
int v[N], w[N];
bool load_data(char* filename) {
string line(256, '\0');
int counter = 0;
// 读文件
ifstream infile;
infile.open(filename);
if(infile){
while ( getline(infile, line) ) {
stringstream s(line);
if(counter == 0){
//s.str(line);
s >> n >> m;
cout << n << "---" << m << endl;
}else{
s >> v[counter] >> w[counter];
cout << v[counter] << "---" << w[counter] << endl;
}
counter++;
}
}
return true;
}
int solve(){
int res = 0;
// initialize
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if( j >= v[i] ){
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
cout << i << "-" << j << " ====> " << f[i][j] << endl;
}
}
}
cout << "==================" << endl;
for (int i = 0; i <= m; i++) {
res = max(res, f[n][i]);
cout << n << "-" << i << " ====> " << f[n][i] << ":" << res << endl;
}
return res;
}
int main(int argc, char *argv[]){
char filename[128] = "data1.1.txt";
int res;
// 加载数据文件
load_data(filename);
// solve
res = solve();
// output
cout << res;
return 1;
}输出
4---5
1---2
2---4
3---4
4---5
1-1 ====> 2
1-2 ====> 2
1-3 ====> 2
1-4 ====> 2
1-5 ====> 2
2-2 ====> 4
2-3 ====> 6
2-4 ====> 6
2-5 ====> 6
3-3 ====> 6
3-4 ====> 6
3-5 ====> 8
4-4 ====> 6
4-5 ====> 8
==================
4-0 ====> 0:0
4-1 ====> 2:2
4-2 ====> 4:4
4-3 ====> 6:6
4-4 ====> 6:6
4-5 ====> 8:8
==================
result : 8算法优化
- f[i][j] = max(f[i-1][j], f[i-1][j-v[i]])
因此f[i][j]只和上一行结果有关,和当前行所有数据无关。因此二维数组可以变为一维数组。
变为一维数组之后,name计算f[j]时候需要f[j-v[i]]的数据。如果我们从左到右逐个计算,当我们计算f[j]的时候,我们实际上获得是第i行的状态,而不是i-1行的状态。所以我们从右向左逐个计算
- 右下角就是最终计算结果,无需遍历
实现
#include <iostream>
#include <cstring>
#include <algorithm>
#include <fstream>
#include <sstream>
using namespace std;
#define MAX_LINE_LENGTH 256
const int N = 1000;
int n, m;
int f[N] = {0}; // 改为一维数组
int v[N], w[N];
bool load_data(char* filename) {
string line(256, '\0');
int counter = 0;
// 读文件
ifstream infile;
infile.open(filename);
if(infile){
while ( getline(infile, line) ) {
stringstream s(line);
if(counter == 0){
//s.str(line);
s >> n >> m;
cout << n << "---" << m << endl;
}else{
s >> v[counter] >> w[counter];
cout << v[counter] << "---" << w[counter] << endl;
}
counter++;
}
}
infile.close();
return true;
}
int solve(){
int res = 0;
// initialize
f[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = m; j >= v[i]; j--) { // 从右到左, j >= v[i]
//f[j] = f[i - 1][j];
//if( j >= v[i] ){
cout<<f[j]<<endl;
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << i << "-" << j << " ====> " << f[j] << endl;
//}
}
}
cout << "==================" << endl;
//for (int i = 0; i <= m; i++) {
// res = max(res, f[i]);
// cout << n << "-" << i << " ====> " << f[i] << ":" << res << endl;
//}
//cout << "==================" << endl;
return f[m];
}
int main(int argc, char *argv[]){
char filename[128] = "data1.1.txt";
int res;
// 加载数据文件
load_data(filename);
// solve
res = solve();
// output
cout << "result : " << res;
return 1;
}